
事实上,无论是德州扑克,还是blackjack而或是各类型的扑克牌游戏,他们的本质都是数学性的,而事实上古老历史的扑克牌和数字,甚至是概率论等学说的提出,有着千丝万缕的联系。
在对冲基金大神Edward Thorp的beat the dealer 一书中,他提到了完整的,应对赌场中21点最完整的一套战略体系,甚至带队杀入赌场,作为一个“离经叛道”的数学家,他决定在LAS VEGAS的赌桌上,甚至是华尔街的金融市场中实践他对数学的理解,应用凯利公式,他在赌场中大杀四方。甚至建立了一个对冲基金Edward Thorp Associates。
从各个角度来说,MIT教授Edward Thorp都是和Taleb Nassim 类似的,skin in the game的实战&理论大师。因此我也受到他们的感染,也想要通过扑克牌,来将概率论,衍生品,甚至是风险管理(risk management)做一个完全的体系化的写作。
这个专题会从不同的游戏出发,同时通过计算不同的概率,甚至是游戏的策略(strategy)并且和案例结合,给到读者全新的,对于数学的全新理解。

有一道关于扑克牌的概率题是我非常喜欢的,曾经跟许多朋友提起。似乎扑克牌永远是概率题目的好基友,翻开一本概率课本,十之八九的问题都是和翻牌洗牌抽牌相关的。这道题是这样的:
有一盒扑克牌,一共 52 张,在经过彻底洗牌后反压置于桌面上。如果某人一次抽取 17 张牌,那么:
1). 在第 17 张牌第一次抽到 A 是概率是多少?
2). 在第 17 张牌第二次抽到 A 的概率是多少?
我们可以这样思考:既然算的是前 17 张牌如何如何的概率,那么后面的 35 张无论怎么抽牌无论抽到怎样的牌都是可以忽略不计的,所以要关注的只有这 17 张牌。两问的样本空间一致,52 选 17 再排列这 17 张牌,
所以 |S| =
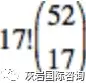
我们先看第一问:在第 17 张牌第一次抽到 A 是概率。也就是说,在这 17 张牌里第 17 张牌肯定是 A,前 16 张都不是 A 却可以是其他的任意牌。
第一步:从 4 张 A 中为第 17 号位置选 1 张
第二步:从 48 张非 A 牌中为前 16 个位置选 16 张
第三步:排列 16 张牌
所以 |E1| =
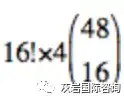
,P1 =

接下来是第二问:在第 17 张牌第二次抽到 A 的概率。那么在这 17 张牌里,最后一张一定是 A,前 16 张里有一张 A 但是位置并不确定,可以在这里也可以在那里。
第一步:从 48 张非 A 牌中为 15 个非 A 的位置选 15 张
第二步:从 4 张 A 中选 2 张
第三步:从选出的 2 张 A 中选一张,与 15 张非 A 组成前 16 张牌
第四步:排列这 16 张牌
第五步:将剩下的那 1 张 A 放到第 17 个位置上
那么 |E2| =
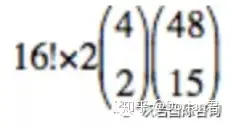
, P2 =

如果追加一问:
3). 在这 17 张牌中有且仅有两个 A 的概率是多少?
有了前两个问的铺垫这个问题就非常简单了。17 个位置里有 2 个 A 但是位置不确定,可以在任意位置被抽到。
第一步:从 48 张非 A 牌中为 15 个非 A 的位置选 15 张
第二步:从 4 张 A 中选 2 张
第三步:排列 17 张牌
因此 |E3| =
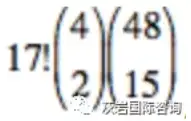
,P3 =

教授曾高深莫测地跟我说,有非常简单精妙的方法可以一击即中,我再三询问他却拒绝透露那个方法究竟是如何地简单精妙。我想了很久百思不得其解,后来在与小 P 的一次闲谈中茅塞顿开。在第一问 “在第 17 张牌第一次抽到 A 是概率是多少” 上,我们的确可以投机取巧。
捷径是:仅仅考虑 4 张 A 的位置,忽略其他所有的非 A 牌。若 52 张牌都被抽取,那么其中会有 4 个位置是 A,若第一次抽到 A 是在第 17 张,那么剩下的 3 张 A 必然是在其后的 35 个位置中。
那么 P1 =
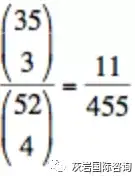
如此一来,省去了许多思考那 17 个位置中非 A 牌该如何如何的过程。虽然前一种方法是正确的,但毕竟颇费功夫。
概率论里有很多有意思的问题。但是无论是摸弹珠还是排小人都无法撼动扑克牌在概率问题里的地位,薄薄的 52 张牌蕴含了许多精妙的理念。如果手里有一盒扑克牌,究竟有多少种排列这 52 张牌的方法呢?答案是 52!,一个表达起来很简单实际上很庞大的数字,至于这个数有多少位数,读者可以具体自行计算。
同时在扑克牌中有一种玩法我觉得很有规律性,也非常适合应用概率论来估算,这种玩法叫“扎金花”或者叫“开拖拉机”。
就是给玩牌的人每人发三张扑克牌,然后每个人根据自己的牌大小在互相不知道大小的情况下下注,最后大者或者胆大者获胜。牌的大小分为单牌、对子、顺子、金花、顺子金花、豹子。
它们的意思分别是单牌:数字没有相同的,花色至少两种;对子:数字有两个是相同的,花色至少两种;顺子:三张牌的数字是连续的,花色至少两种;金花:数字没有相同的,花色只有一种;顺子金花:三张牌的数字是连续的,花色只有一种;豹子:三张牌的数字一样,花色有三种(牌的数字是指从A、2、3、4、5、6、7、8、9、10、J、Q、k)(牌的花色是指黑桃、红桃、方块和梅花四种,事件由一副牌发生,而且去掉了两个王只有52张牌)。
现在就来分析这种古典型概率事件的发生概率:
一、一副牌中摸到三张K的概率
第一次摸牌是从52张牌中抽取黑桃、红桃、方块和梅花中的一张K,抽中的概率是52分之4;第二次摸牌是从余下的51张牌中抽取余下的三张中的一张K,发生的概率是51分之3;第三次摸牌是从余下的50张牌中抽取余下的两张中的一张K,发生的概率是50分之2。所以,一副牌中同时摸到三张K的概率是它们的积:
(4/52)×(3/51)×(2/50)=24/132600
二,一副牌中摸到豹子的概率
由于摸到豹子K的概率已经算出是24/132600,那么摸到三张A(豹子A)的概率也是24/132600,摸中2、3、4、5、6、7、8、9、10、J、Q的概率都是24/132600,也就是说摸中从A到K共13种牌型的总概率为它们之和。即一副牌中摸到豹子的概率是:
13×(4/52)×(3/51)×(2/50)=312/132600=1/425
即就是说大约摸425次牌可以出现一次豹子。
三,一副牌摸中全部是红桃(金花)的概率
第一次摸牌是从52张牌中抽取13张红桃中的一张,抽中的概率是52分之13;第二次摸牌是从余下的51张牌中抽取余下的12张红桃中的一张,发生的概率是51分之12;第三次摸牌是从余下的50张牌中抽取余下的11张红桃中的一张,发生的概率是50分之11。所以,一副牌中同时是红桃(金花)的概率是它们的积:
(13/52)×(12/51)×(11/50)=1716/132600
即就是说大约摸78次牌可以出现红桃金花。
四,一副牌摸中全部是金花的概率
出现红桃金花的概率是1716/132600,同样的道理,出现黑桃、方块和梅花金花的概率也是1716/132600。所以出现金花的概率是:
4×(13/52)×(12/51)×(11/50)=6864/132600
所以,金花出现的概率大约是20次就出现一次金花,是豹子出现概率的22倍。
五,一副牌摸中顺子234的概率
第一次摸牌是从52张牌中抽取黑桃、红桃、方块和梅花四张2中的一张,抽中的概率是52分之4;第二次摸牌是从余下的51张牌中抽取黑桃、红桃、方块和梅花四张3中的一张,发生的概率是51分之4;第三次摸牌是从余下的50张牌中抽取黑桃、红桃、方块和梅花四张4中的一张,发生的概率是50分之4。所以,一副牌是顺子234的概率是它们的积:
(4/52)×(4/51)×(4/50)=64/132600
即就是说大约摸2072次牌可以出现顺子234。
六,一副牌摸中顺子的概率
由于摸中顺子234的概率是64/132600,那么有多少顺子呢,有A23、234、345、456、567、678、789、8910、910J、10JQ、JQK,一共是十一(13减3加1)种顺子,所以在以上计算的基础上乘11。所以,一副牌是顺子的概率是:
11×(4/52)×(4/51)×(4/50)=704/132600
即就是说大约摸189次牌可以出现一次顺子。是金花出现概率的9分之一。
七,一副牌摸中对子K的概率
第一次摸牌是从52张牌中抽取黑桃、红桃、方块和梅花中的一张K,抽中的概率是52分之4;第二次摸牌是从余下的51张牌中抽取余下的三张中的一张K,发生的概率是51分之3;第三次摸牌是从余下的50张牌中抽取余下50张牌的除过K以外任意一张,发生的概率是50分之48。所以,一副牌中同时摸到对子K的概率是它们的积:
(4/52)×(3/51)×(48/50)=576/132600
八,一副牌摸中对子的概率
由于摸到对子K的概率已经算出是576/132600,那么摸到对子A(豹子A)的概率也是576/132600,摸中2、3、4、5、6、7、8、9、10、J、Q对子的概率都是576/132600,也就是说摸中从A到K共13种牌型的总概率为它们之和。即一副牌中摸到对子的概率是:
13×(4/52)×(3/51)×(48/50)=7488/132600=1/18
即就是说大约摸18次牌可以出现一次对子。
九,出现金花顺子红桃234的概率是
(1/52)×(1/51)×(1/50)=1/132600
出现红桃123,234,345,456,567,678,789,8910,910J,10JQ,JQK的概率是:
11×(1/52)×(1/51)×(1/50)=11/132600
出现黑桃、红桃、方块和梅花123,234,345,456,567,678,789,8910,910J,10JQ,JQK的概率是:
4×11×(1/52)×(1/51)×(1/50)=44/132600
就是说每3014次才能摸到一次金花顺子。
其它情况下就是摸到单牌的概率,通常情况下人们对此不感兴趣,所以不再计算。
综上所述,对子出现概率是1/18,金花出现的概率是1/20,顺子出现的概率是1/189,豹子出现的概率是1/425,金花顺子出现的概率是1/3014。所以金花顺子出现的概率最小。
以上所讲简单易懂,对于初学者很好掌握,但是缺点是不够专业,而且计算复杂麻烦,如果用这种方法计算别的概率问题很容易错误。所以有必要把以上概率问题使用较为专业的术语和方法加以整理。
首先一个问题:玩扑克牌是排列问题还是组合问题?从52张扑克中发给3张牌,考虑不考虑这3张牌的发牌顺序问题?例如发了个234,那么是2先发的,还是4先发的?如果考虑发牌顺序,那么三张牌的顺序就是3×2×1种排列(用3!表示,读作3的阶乘,又叫全排列),就是排列问题,从52张扑克中发给3张牌用P523表示,意思是52×51×50,用阶乘表示就是52的阶乘除以52-3=49的阶乘,即52!/49!。
通常情况下,人们对于发牌顺序不感兴趣,只对是不是234感兴趣,所以不考虑发牌顺序问题,这个问题就是数学上的“组合”问题,组合问题一般用C表示,例如从52张牌中发取3张,它的可能性就是C523,其实就是P523/3!,即52!/(49!×3!)。
通常情况下从M个总体中不返回地抽取N个样本进行排列用公式PMN表示,它就等于M!除以(M-N)!,如果从M个总体中不返回地抽取N个样本进行组合用公式CMN表示,它就等于M!除以(M-N)!再除以N!。很显然组合并不考虑N个样本内部的顺序问题,所以它比排列取得的数字小,但是得到的概率大。
第二个问题,玩扑克牌是返回抽样还是不返回抽样?
发牌的时候考虑不考虑余下的牌的数量问题?
实际上不管多少人玩扑克,发出去的扑克不再收回,发出去的牌和留下的扑克的总数是52,这种发牌就是抽取样本的一种方式叫“不返回抽样”。只有不返回抽样的计算才能用到排列组合知识。如果不是不返回抽样,就叫“返回抽样”,例如给某个人算命抽签,当抽取64卦中的一个签之后得到卦辞,然后把签放回去再抽取,它得到的概率永远是1/64。返回抽样的计算方式相对简单,不需要排列组合公式。我们在玩三叶牌的游戏时是典型的“不返回抽样”。
第三,玩扑克是典型的古典型概率问题。
什么是古典型概率,古典概型具备两个条件:
1,样本空间的元素只有有限个,在扑克牌中样本数量为52;
2,每个基本事件出现的可能性是相等的,在扑克牌中抽取到某个扑克的概率都是一样的。所以古典概型又叫等可能概型。
由于在现实中遇到的概率问题中,样本的数量往往是不确定的,每个基本事件出现的可能性是不相等的,所以大多数概率问题不是古典概型。如果样本的数量往往是无限多的,每个基本事件出现的可能性是相等的,那么可以用几何的方法来计算其概率问题,可以称为几何分布。“自有限总体的不还原抽样得到的一元离散型概率分布”叫超几何分布,它们需要组合公式来计算。扑克牌基本符合超几何分布,但是它是二元分布。
第四,扑克牌中的概率问题是离散型概率还是连续型概率。
离散型概率问题是和连续型概率问题相对应的。常用的离散型概率概型(分布)有两点分布、二项分布、超几何分布、泊松分布、几何分布。两点分布又称伯努利分布,在每次试验中只有两种可能的结果,而且是互相对立的,是独立的,与其它各次试验结果无关,结果事件发生的概率在整个系列试验中保持不变,则这一系列试验称为伯努力试验。
二项分布即重复n次的伯努利试验,它就是“自有限总体的还原抽样得到的一元离散型概率分布。“自有限总体的不还原抽样得到的一元离散型概率分布”叫超几何分布。泊松分布其实是二项分布在样本很大的情况下的一种理论近似,它的参数λ就是它的期望和方差,一般随机质点流符合泊松分布。附和泊松分布的随机质点流也叫泊松随机质点流,也叫泊松流。例如把玩扑克的时候黑桃K到某个人的手里的次数随着时间推移所形成的随机质点流可以认为是泊松流。离散型概率的计算和连续性概率不同之处在于,离散型概率的计算可以用枚举法来分析。在这里玩扑克的时候就是具体的枚举分析。
现在我们应用组合公式对玩金花的概率问题重新分析。扑克牌有黑桃、红桃、方块和梅花四种牌型,有从A、2、3、4、5、6、7、8、9、10、J、Q、K总共13种数字,我们称为13种数型。
一,一副牌中摸到三张K的概率
其数型只有一种,牌型有4种,从四种牌型中抽取三种进行组合,所以是C43,而52张牌中抽取3张的组合是C523,所以发生的概率是C43/C523,答案是24/132600。和分析法计算值一样。
二,一副牌中摸到豹子的概率
其数型是13种数型中取一种,所以其数型为C131,其它计算和摸到三张K的概率计算一样,发生的概率是C131×C43/C523,答案是312/132600=1/425。和分析法计算值一样。
三,一副牌摸中全部是红桃(金花)的概率
其数型有3种,从13张牌中抽取3种数型进行组合C133,牌型有1种,而52张牌中抽取3张的组合是C523,所以发生的概率是C133/C523,答案是1716/132600。和分析法计算值一样。
四,一副牌摸中全部是金花的概率
其数型有3种,从13张牌中抽取3种数型进行组合C133,牌型有4种,从4种牌型中选取1种牌型,所以是C41,而52张牌中抽取3张的组合是C523,所以发生的概率是C41×C133/C523,答案是6864/132600。和分析法计算值一样。
五,一副牌摸中顺子234的概率
其数型其实只有一种,但是三种数字的组合,每一种数字出现的牌型有4种,组合是C41,有3个数字,所以234的组合数量为C41×C41×C41,而52张牌中抽取3张的组合是C523,所以发生的概率是C41×C41×C41/C523,答案是64/132600。
六,一副牌摸中顺子的概率
顺子其实是一种数字组合,其数型其实有(13-3+1)=11种,从这11种数型中选取一种才成为顺子,所以其组合为C111, 在这个顺子组合中,每一个元素的牌型都是4种,从4种牌型中抽取一种,组合是C41,有3个数字,所以顺子内部的组合数量为C41×C41×C41, 而52张牌中抽取3张的组合是C523,所以发生的概率是C111×C41×C41×C41/C523,答案是704/132600。
七,一副牌摸中对子K的概率
在这种牌型中,3张牌实际上分为两个类型,第一种是对子,牌型是4选2,数型只有一种K,而52张牌中抽取2张的组合是C522,发生的概率是C42/C522,第二种类型是一张任意牌,牌型是4选1,组合是C41,数型是12选1(除过K),组合是C121,是从余下的50张牌中选取,所以组合C41×C121/C501,所以发生的概率是两种组合的乘积,是(C42/C522)×(C41×C121/C501),答案是576/132600。和分析法计算值一样。
八,一副牌摸中对子的概率
在这种牌型中,3张牌实际上分为两个类型,第一种是对子,牌型是4选2,数型是13选1,而52张牌中抽取2张的组合是C522,发生的概率是C42×C131/C522,第二种类型是一张任意牌,牌型是4选1,组合是C41,数型是12选1(除过K),组合是C121,是从余下的50张牌中选取,所以组合C41×C121/C501,所以发生的概率是两种组合的乘积,是(C42×C131/C522)×(C41×C121/C501),答案是7488/132600=1/18。
九,出现金花顺子红桃234的概率是
在这里,牌型只有一种,数型只有一种数字组合,也只有一种(在数字组合内部每一种数字出现的牌型只有1种,数型只有一种),所以它的概率是52选3中的一种,为1/C523=1/132600,
十,出现红桃顺子的概率:
顺子其实是一种数字组合,其数型其实有(13-3+1)=11种,从这11种数型中选取一种才成为顺子,所以其组合为C111,出现红桃顺子的概率C111/C523=11/132600
十一,出现金花顺子的概率:
这时候牌型是4选1,数型是数字组合11选1,从52张牌中抽取3张(当然也可以分别抽取),所以出现红桃顺子的概率C41×C111/C523=44/132600
就是说每3014次才能摸到一次金花顺子。
金花顺子实际上是一个条件概率,是求在顺子的条件下的金花的概率,或者是求在金花的条件下的顺子的概率。我们用条件概率公式来求证一下。金花出现的概率是6864/132600,金花中的牌型只有一种,这时候主要是数型发生了变化,而且顺子的概率从组合问题转化为排列问题,因为此时必须考虑3张牌的排列顺序,所以要求从P133个排列中取出(13-3+1)种典型排列,所以它的概率是P111/P133=1/156,所以在金花条件下顺子的概率是6864/(132600×156)==44/132600。
顺子出现的概率是704/132600,顺子中出现金花的要求是第二张和第三张牌的牌型和第一张牌的牌型保持一致,因此牌型从C41×C41×C41改变为C41×C11×C11,因此概率减小16倍,704/(132600×16)=44/132600。